嗷,看到标题直接劝退?不不不,不许划走!给我回来!
说到加密……
大家应该都不陌生吧?二战时期就已经有了恩尼格玛密码机(虽然最后被图灵破了),而现在,各种加密算法更是层出不穷,其中最有名的,应该就是RSA非对称加密算法了。那么,问题来了【直奔主题】。
都有哪些种类的加密算法?RSA又是什么?
先来回答第一个问题:加密算法共分为两种:对称加密和非对称加密。

而RSA,则是非对称加密的代表 “人物”,大部分甚至全部SSL协议的加密算法用的都是它。它的具体加解密过程如下:
‘’ 现在我们来详细叙述一下RSA加密算法,它是所谓的非对称加密,也就是说,RSA的使用者拥有两个协同使用的密钥:公钥e和私钥d。重要的是,给定公钥e,用户可以先秘密选取两个足够大的素数p和q,然后迅速计算出与公钥e对应的私钥d,更准确地说,用户应该计算出满足 ed = 1 mod (p-1)(q-1)的d值,可以利用欧几里得算法对e和(p-1)(q-1)的最大公因数计算得到。然而,为了让其他人能够向自己发送加密信息,用户应该同时披露这两个素数的乘积 N = pq。这样的话,如果攻击者能够将N分解为两个素数p和q的乘积的话他就可以按照用户执行过的步骤,根据公钥e迅速计算出私钥d,这样他就破译了RSA加密算法。‘’
–摘自《贝叶斯的博弈:数学、思维与人工智能》
没看懂?嗷,没事,其实我也没看懂,下面就来 ” 详解 ” 一下RSA的加解密过程!
首先需要明确几个数学概念:
· 素数(质数)
· 互质数
· 模指数运算(***重点***)
1.素数(质数):
质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数(1既不是质数也不是合数)。
例如,15=3*5,所以15不是质数;又如,12=6*2,所以12也不是质数。而13除了等于13*1以外,不能再表示为其它任何两个整数的乘积,所以13是一个质数。
质数有无限个。
2.互质数
小学数学教材中对互质数是这样定义的:公因数只有1的两个数,叫做互质数(这里所说的 ” 两个数 ” 是指自然数)。
两数互质的几种情况:
①.任意两个质数都是互质关系
②.如果两个数之中,较大的那个数是质数,则两者构成互质关系
③.如果两个数之中,较小的那个数是质数,且较大数不为较小数的整数倍,则两者构成互质关系
④.1和任意一个自然数是都是互质关系
⑤.p是大于1的整数,则p和 (p-1) 构成互质关系
⑥.p是大于1的奇数,则p和 (p-2) 构成互质关系
3.模指数运算(***重点***)
指数运算(幂运算):
幂运算是一种关于幂的数学运算(这不是废话吗??啊?百度?出来解释一下?)。
运算法则:
①.同底数幂相乘,底数不变,指数相加。
②.同底数幂相除,底数不变,指数相减。
③.幂的乘方,底数不变,指数相乘。
具体见下图:

模运算(mod):
” 模 ” 是英语 ” Mod ” 的音译,即取余。
模运算是整数取余运算(在Python中用%表示)。如:有一个整数m,以n为模做模运算,即m mod n,只需让m去被n整除,取所得的余数作为结果即可。具体见下图(自己做的图,嘿嘿):

好啦,现在开始正式 ” 讲解 ” RSA加密算法啦咯~!
算法描述:
(1)选择两个不同的、足够大的素数p、q。
(2)计算N = pq。
(3)计算 f(n) = (p-1)(q-1),同时对p、q严加保密,不让任何人知道。【f(x)代表一个函数,当自变量x=n的时候即可写成 f(n)】
(4)找一个与 f(n) 互质的数e,且1< e < f(n)。
(5)计算d,使得 ed ≡ 1 mod f(n)。这个公式也可以表达为 d ≡ e-1 mod f(n)
注:≡ 是数论中表示同余的符号。公式中,≡ 符号的左边必须和符号右边同余,也就是两边模运算结果相同。
显而易见(并不),不管 f(n) 取什么值,符号右边1 mod f(n) 的结果都等于1;故符号的左边d与e的乘积和 f(n) 做模运算后的结果也必须等于1。这就需要计算出d的值,让这个同余等式能够成立。
(6)公钥KU=(e, n),私钥KR=(d, n)。
(7)加密时,先将明文变换成0至 (n-1) 的一个整数M。若明文较长,可先分割成适当的组,然后再进行交换。设密文为C,则加密过程为:C ≡ Me(mod n)
(8)解密过程为:M ≡ Cd(mod n)
完成!!!
嗷,由于我水平有限,无法理解更无法给出RSA的严格数学证明及逻辑证明,但我们可以通过一个简单的例子来理解和模拟RSA的工作原理。为了便于计算。在这个例子中只选取小数值的质数p、q、e。
例子开始:
假设Alice需要将明文 ” ltx ” 通过RSA加密后传递给Bob(上面说过, 在密码学中,通信双方分别叫Alice和Bob),过程如下:
Step ①. 设计公私密钥(e, n)和(d, n):
令 p=3,q=11,得出N=pq=3×11=33;f(n)=(p-1)(q-1)=2×10=20;取e=3,(3与20互质且1<3<20)则ed ≡ 1 mod f(n),即3·d ≡ 1 mod 20。
d怎样取值呢?可以用试算的办法来寻找(咳咳,那叫枚举!!)。枚举试算结果见下表:
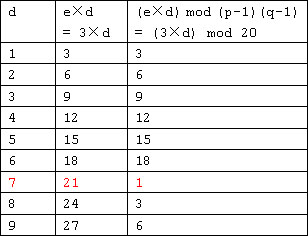
耶!!我们找到了!!当d=7时,ed ≡ 1 mod f(n) 同余等式成立。因此,可令d=7。从而我们可以设计出一对公私密钥:
加密密钥(公钥)为:KU =(e, n)=(3,33),解密密钥(私钥)为:KR =(d, n)=(7,33)。
Step ②. 英文数字化:
将明文信息数字化,并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值,即:

则得到分组后的 ” ltx” 的明文信息为:12,20,24。
Step ③. 明文加密:
用加密密钥 (3, 33) 将数字化明文分组信息加密成密文。由 C ≡ Me(mod n) 得:
C1 (密文) ≡ M1(明文)^e (mod n)= 11(11 ≡ 12^3 mod 33)
C2 (密文) ≡ M2(明文)^e (mod n) = 7 (7 ≡ 20^3 mod 33)
C3 (密文) ≡ M3(明文)^e (mod n) = 15 (15 ≡ 24^3 mod 33)
所以密文为11、7、15(啊啊啊我身为一名数竞玩家这个计算居然看 & 算了十多分钟才搞明白啊啊啊数竞数竞我不配)。
Step ④. 密文解密:
用解密密钥 (7, 33) 对密文进行解密。由 M ≡ Cd(mod n) 得:
M1 (明文) ≡ C1(密文)^d (mod n) = 12(12 ≡ 11^7 mod 33 )
M2 (明文) ≡ C2(密文)^d (mod n) = 20(20 ≡ 7^7 mod 33)
M3 (明文) ≡ C3(密文)^d (mod n) = 24(24 ≡ 15^7 mod 33)
嗷嗷!!根据上面的编码表将其转换为英文,我们又得到了恢复后的原文 ” ltx “!!(天啊我真的太激动了!!)
当然,实际运用要比这复杂得多,由于RSA算法的公钥私钥的长度(模长度)要到1024位甚至2048位才能保证安全,因此,p、q、e的选取、公钥私钥的生成,加密解密模指数运算都有一定的计算程序,需要依仗计算机高速完成。
最后,我们再来简单谈谈RSA的安全性。
为什么RSA密码难于破解?
在RSA密码应用中,公钥KU是被公开的,即e和N的数值可以被第三方窃听者(密码学中称为Eve)得到。破解RSA密码的问题就是从已知的e和N的数值(N = pq),设法求出d的数值,这样就可以得到私钥来破解密文。
从上文中的公式:d ≡ e-1 (mod((p-1)(q-1))) 或 de ≡ 1 (mod((p-1)(q-1))) 我们可以看出,密码破解的实质问题其实就是:
求出 (p-1) 和 (q-1) 。
换句话说,只要求出p和q的值,我们就能进而求出d的值而得到私钥。
当p和q是一个足够大的素数的时候,通过它们的积pq去分解因子p和q,这是一个公认的数学难题。比如当pq大到1024位时,迄今为止还没有人能够利用任何计算工具去完成分解质因数的任务。因此,RSA从提出到现在已近20年,经历了各种攻击的考验,逐渐被人们所接受。普遍被认为是目前最优秀的加密方案之一。
然而,虽然RSA的安全性依赖于大数的因子分解,但并没有从理论上证明破译RSA的难度与大数分解难度等价。即:
RSA的重大缺陷是无法从理论上把握它的保密性能如何。
此外,RSA的缺点还有:
①. 产生密钥很麻烦。受到质数产生技术(鹅鹅鹅这是我自创的名词)的限制,因而难以做到一次一密。
②. 分组太长。为保证安全性,N至少也要 600 bits 以上,这便导致运算代价很高。而这个缺陷主要反映在了加解密速度上。RSA的时间复杂度较对称加密算法慢了好几个数量级(1500倍)!且随着大数分解技术的发展,这个长度还在增加,不利于数据格式的标准化。因此,RSA只能用于加密少量数据,大量的数据尤其是文件的加密还是需要借助对称加密算法。
但是…对大数进行分解质因数…就真的不可行吗…
有一种计算机,叫量子计算机…
那么,下一篇文章,我们就来看一看,量子计算机的问世,是否会对RSA产生(毁灭性的)影响??
小彩蛋:
图为RSA的三位发明者,从左到右分别是Ron Rivest、Adi Shamir、Leonard Adleman,照片摄于1978年。
(把这三个人姓的首字母连起来,看看你发现了什么?)
(其实我很好奇,如果当年他们三个换个方式照相,那这个算法是不是就要改名了?)

嗷,明天再见啦!
2021-08-20(22:56)
By 代码一姐



小彩蛋蓝桥杯考过……我直接把选项的名字翻译成英文做的……Git的SSH key也是基于RSA!!
另:速度不错!
666可以的,给你点一个大大的赞
嗷,谢谢鸭!
PS:我的smtp搞好啦(但是有亿点点慢啊啊啊啊),你可以去注册啦!
小彩蛋在蓝桥杯考过……要是当时看过这篇文章就好了……它问哪个不是RSA创始人,我当时直接硬翻译选项上的名字……而且Git的SSH应该也是RSA耶!真是应用很广泛呢。
注:网站速度不错!!
对呀对呀,还有SSL协议,都是用的RSA!
啊啊啊我严重怀疑我这个网站就是间歇性抽风。。。。
一会儿一下就打开了,一会儿转圈圈转好久。。
我尝试分析过不少原因,带宽和时延?时间复杂度?多线程导致的慢?
Aaaaa!!!
really? 那可不好。不过maybe i can help. 那个啥, “抽风”的时候麻烦杰哥评(截屏)你的页面, 然后右键, 点击“检查”, 在侧栏上面从elements 改为console, 杰哥评, “让我看看”, 也许我能排查出问题。
p.s. 我这里 显示你的网站一直超勇的。你可以尝试清除浏览器缓存, 看是否解决。
ummm…你还在搞cloudflare 吗?
欧克欧克,什么时候出问题了我就杰哥评给你,嘿嘿嘿…..
对了,***,” 让我看看 ” 这个梗……
不要以为我不懂….
嘻嘻…….
【笑容逐渐奇怪~~~】
cloudflare刚刚开始弄,我觉得我真的太有必要去搞一个Google账号了嗷!!!
好啦,曹智杰同学,晚安咯~~
【让 我 看 看】
-让我康康
-不要
-有一个杰哥前来买瓜
-哥俩生异性吗
……
-杰哥:你要不要吧
-阿伟:不要
……
你tm劈我瓜是不
…..
萨日朗g!!!!
(这是两个梗结合在一起后的故事[doge])
我表示我没看懂、。。。。
啊啊啊我是不是跟不上时代了啊啊啊啊啊啊
【抓狂.jpg】
那么,刘陈杰同学(咳咳,我故意的,让你成为杰哥),解释一下~~??
【逐渐怪异的笑容】
好家伙